Prawda jak byt mieni się wielorako. W metafizyce mówi się o prawdzie ontycznej czyli „zgodności rzeczy z myślą" lub o prawdzie jako własności samego bytu. Teoria poznania odsyła do klasycznej definicji prawdy, zwanej Arystotelesowską, zgodnie z którą „prawdą jest powiedzieć o czymś, że jest, jeśli jest i że nie jest, jeśli nie jest" oraz definicji koherencyjnej i pragmatycznej. Za główne kryteria prawdy najczęściej przyjmuje się oczywistość, doświadczenie, praktykę lub poznawczą użyteczność. Wiek XX, to wiek, w którym głównym przedmiotem zainteresowania filozofów stał się język. Prawda zatem stała się zagadnieniem rozważanym przede wszystkim w obrębie semantyki. Do tego nurtu należą również poświęcone problemowi prawdy badania Tarskiego. Badania te, jak spróbuję krótko pokazać na końcu pracy, stały się inspiracją dla wielu współczesnych myślicieli.

Tarski jest autorem dwóch teorii prawdy: syntaktycznej i semantycznej. Teoria syntaktyczna jest mniej znana i jej rozwój i praktyczne konsekwencje nie były przedmiotem zainteresowania wielu badaczy. Najlepsze jej rozwinięcie znajdujemy w systemach Leśniewskiego: prototetyce, ontologii i mereologii. Tworząc swoje systemy Leśniewski oparł się na definicji prawdy sformułowanej przez Tarskiego w jego pracy doktorskiej ^{[ 1 ]}:

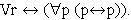
W powyższej syntaktycznej definicji, prawda jest równoważna elementarnej tautologii logicznego systemu. A ponieważ wszystkie systemy Leśniewskiego są zupełne i niesprzeczne, wobec tego każde zdanie prawdziwe można uzyskać jako tezę systemu. Oto definicja zdania prawdziwego w języku prototetyki (w pozostałych językach — ontologii i mereologii — definicja ta wygląda tak samo):  

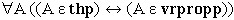
gdzie 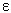oznacza „jest", thp oznacza „teza prototetyki", vrpropp oznacza „zdanie prawdziwe". Słownie: dla każdego A, A jest tezą prototetyki wtedy i tylko wtedy, gdy A jest zdaniem prawdziwym. ^{[ 2 ]}

Semantyczna teoria prawdy Tarskiego często bywa opisywana jako wersja klasycznej definicji prawdy. Przedstawienie i badania związane z semantyczną teorią prawdy znajdują się wpracach Tarskiego, wydanych jako Pisma logiczno — filozoficzne, tom 1 — prawda. Główną tezą, którą uzasadnia i rozwija tam polski logik, jest stwierdzenie, że nie da się zbudować poprawnej definicji zdania prawdziwego dla języka potocznego oraz dla języków nieskończonego rzędu sformalizowanych nauk dedukcyjnych. Definicję taką można zbudować jedynie dla języka skończonego rzędu w systemie dedukcyjnym. ^{[ 3 ]}

Tarski buduje definicję dla bardzo elementarnego systemu, stwierdzając, że można analogicznie zbudować podobną definicję w systemach bogatszych (ściślej: w takich, w których rząd zmiennej rozumiany w znaczeniu teorii typów nie przekracza pewnego z góry danego n będącego liczba naturalną). Zaczyna od rozróżnienia dwóch języków: języka, w którym mówimy, oraz języka, o którym mówimy. Zdanie, którego prawdziwość będziemy definiować, należy do języka, o którym mówimy. Sama definicja będzie jednak należeć do języka, w którym mówimy.

Tarski tworzy zatem, bardzo prosty język, o którym mówimy. Zawiera on: trzy zmienne a, b, c, termin pierwotny „jest częścią", terminy logiczne: negację, alternatywę, kwantyfikator ogólny oraz nawiasy. Tarski nie podaje precyzyjnej aksjomatyki systemu, wyróżnia natomiast funkcje pierwszego rzędu (elementarne), czyli inkluzje (stwierdzenia „jest częścią"). Funkcje drugiego rzędu tworzymy łącząc funkcje pierwszego rzędu za pomocą jednego terminu logicznego. Analogicznie tworzy funkcje dowolnego rzędu naturalnego. Funkcje zdaniowe języka, o którym mówimy, nie posiadające zmiennych wolnych, noszą nazwę zdań.

Język, w którym mówimy zawiera: wyrażenia równoznaczne z wyrażeniami języka, o którym mówimy (np. jest częścią, lub), wyrażenia z₁, z₂, z₃ (które oznaczają kolejno zmienne a, b, c), funkcję nazwową I(x,y), której argumentami są z₁, z₂, z₃, a wartościami odpowiednie inkluzje, wyrażenia: nieprawda, że x, suma logiczna x i y oraz generalizacja wyrażania y ze względu na x (np. (dla każdego x) y). I_n,p jest równoznaczne z I(z_n,z_p), gdzie n, p = 1, 2, 3. Chcąc skonstruować definicję zdania prawdziwego Tarski, posługuje się pojęciem spełniania funkcji zdaniowej przez ciąg przedmiotów. W sposób indukcyjny określamy, kiedy pewien ciąg przedmiotów spełnia funkcje zdaniową n - tego rzędu. W pierwszym kroku indukcyjnym stwierdzamy, że ciąg C spełnia inkluzję I_n,p wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) n, p = 1, 2, 3; (3) n — ty wyraz ciągu jest częścią p - tego wyrazu ciągu, czyli zachodzi inkluzja I(C_n,C_p). W drugim kroku Tarski stwierdza, że aby określić, kiedy ciąg C spełnia funkcje zdaniowe wyższego rzędu, należy jedynie określić, kiedy C spełnia negację, sumę i generalizację funkcji pewnego rzędu, jeśli wiadomo (z założenia indukcyjnego), że spełnia funkcje tego rzędu. C spełnia negację x wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) ciąg C nie spełnia x. C spełnia x + y wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) ciąg C spełnia x lub spełnia y. Ciąg C spełnia generalizację x ze względu na n-tą zmienna wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) n, p = 1, 2, 3; (3) zarówno C, jak i każdy inny ciąg otrzymany z C przez zmianę tylko n — tego wyrazu, spełnia x. Zdania języka, o którym mówimy, są pewnymi funkcjami zdaniowymi, zatem możemy podać następującą definicję zdania prawdziwego: Zdanie z języka, o którym mówimy, jest prawdziwe wtedy i tylko wtedy, gdy każdy ciąg spełnia to zdanie. Definicja ta jest, zdaniem Tarskiego, dobra, ponieważ: (1) jest zgodna z intuicyjnym rozumieniem słowa prawdziwość; (2) jest przy niej spełniona zasada wyłączonego środka; (3) jest przy niej spełniona zasada sprzeczności; (4) pozwala udowodnić niesprzeczność rozważanego systemu.

Jak zbudować definicję zdania prawdziwego w pewnych systemach dedukcyjnych skończonego rzędu Tarski pokazuje na przykładzie języka algebry klas. Ważnym elementem tej definicji jest umowa P, która powiada: poprawną formalnie definicję symbolu „Vr" (klasa wszystkich zdań prawdziwych), sformułowaną w terminach metajęzyka, nazywać będziemy trafną definicję prawdy, o ile pociąga ona za sobą następujące konsekwencje: (a) wszystkie zdania dające się uzyskać z wyrażenia „x należy do Vr wtedy i tylko wtedy, gdy p" przez zastąpienie symbolu „x" nazwą strukturalnoopisową dowolnego zdania rozważanego języka, zaś symbolu "p" — wyrażeniem, stanowiącym przekład tego zdania na metajęzyk; (b) zdanie "dla dowolnego x — jeśli x należy do Vr, to x należy do S" lub innymi słowy, "Vr należy do S". ^{[ 4 ]}

Aby uzasadnić, że nie da się skonstruować definicji prawdy dla wszystkich języków nieskończonego rzędu, Tarski powołuje się na logika austriackiego, Kurta Goedla. Wykazał on, że w jednym z takich języków — arytmetyce, nie da się skonstruować ścisłej definicji prawdy. Twierdzenie Goedla w wersji formalnej brzmi: w każdym niesprzecznym systemie formalnym obejmującym arytmetykę istnieją arytmetyczne prawdy, których nie można udowodnić w ramach tego systemu. Twierdzenie to ma dwie wersje: pierwszą mówiącą o niezupełności systemów dedukcyjnych zawierających arytmetykę liczb naturalnych oraz drugą stwierdzającą niemożliwość przeprowadzenia dowodu niesprzeczności (spójności) systemów zawierających arytmetykę liczb naturalnych przy pomocy środków samych tych systemów.

Dowód twierdzenia Goedla jest bardzo skomplikowany, dlatego spróbuję tylko przybliżyć jego ideę. Goedel zwrócił uwagę, iż każdy system formalny dowolnej dziedziny matematyki sam też jest obiektem matematycznym. Można zatem arytmetycznie przedstawić dowolny system formalny, który ma obejmować arytmetykę. Mówiąc inaczej, znalazł sposób przedstawienia wszystkich stwierdzeń o liczbach i związkach między liczbami za pomocą liczb. ^{[ 5 ]}. Goedel wprowadził taki wariant numerowania, by zakodować wszystkie możliwe stwierdzenia arytmetyczne w języku samej arytmetyki. Punktem wyjścia były dla niego „Principia Mathematica" B. Russella i Alfreda Northa Whiteheada, które były próbą zapisu matematyki jako zaksjomatyzowanego systemu formalnego. Goedel określił sposób arytmetycznego kodowania wszystkich symboli i stwierdzeń języka Russella — Whiteheada. Założył, że istnieje 10 znaków logicznych, którym odpowiadają pewne numery (nazwane później numerami Goedla) — liczby całkowite od 1 do 10:

Znak	Numer Goedla	Znaczenie
~	1	Nie
V	2	Lub
→	3	Jeżeli… to...
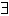	4	Istnieje
=	5	Równa się
0	6	Zero
S	7	Bezpośredni następnik
(	8	Znak interpunkcyjny
)	9	Znak interpunkcyjny
'	10	Znak interpunkcyjny

Oprócz tych elementarnych zmiennych język „Principia Mathematica" zawierał zmienne logiczne łączone za pomocą znaków. Zmienne te można podzielić na trzy rodzaje:

1. zmienne liczbowe, kodowane za pomocą liczb pierwszych większych od 10, czyli 11, 13, 17, 19,...

2. zmienne zdaniowe — wyrażenia logiczne i wzory, kodowane za pomocą kwadratów liczb pierwszych większych od 10, czyli 11², 13², 17², 19², ...

3. predykaty — właściwości liczb, wyrażeń liczbowych, kodowane za pomocą sześcianów liczb pierwszych większych od 10, czyli 11³, 13³, 17³, 19³, ...

Dla przybliżenia problemu rozważmy wyrażenie logiczne: (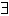x)(x = sy), które czytamy istnieje x taki, że x jest bezpośrednim następnikiem y. x, y to zmienne liczbowe, zatem zgodnie z procedurą kodowania mamy x - 11, a y — 13, ponieważ 11 i 13 to dwie najbliższe liczby pierwsze większe od 10. Teraz podstawiamy za kolejne symbole liczby kodujące otrzymujemy sekwencję: (8, 4, 11, 9, 8, 11, 5, 7, 13, 9). Aby teraz otrzymać z tego konkretną liczbę, która będzie kodowała to twierdzenie i tylko to twierdzenie, bierzemy 10 kolejnych liczb pierwszych (ponieważ nasza sekwencja składa się z 10 liczb) poczynając od 2. Następnie podnosimy każdą liczbę pierwszą do potęgi równej liczbie kodującej odpowiedni symbol w wyrażeniu, a potem mnożymy je. Otrzymana liczba będzie wzajemnie jednoznacznie przyporządkowana wyrażeniu, ze względu na matematyczne twierdzenie o jednoznaczności rozkładu. Spójrzmy jeszcze na wyrażenie podane w przykładzie:

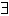(x)(x = sy) → 2⁸·3⁴·5¹¹·7⁹·11⁸·13¹¹·17⁵·19⁷·23¹³·29⁹

Kluczowym elementem dowodu I Twierdzenia Goedla o niezupełności było znalezienie sposobu kodowania arytmetycznego takich różniących się semantycznie poziomów wyrażeń logicznych. Zatem za pomocą systemu Goedla można wyrazić każde stwierdzenie o liczbach naturalnych w postaci pewnej liczby naturalnej, co umożliwia wykorzystanie do badania prawd arytmetycznych arytmetyki. W II Twierdzeniu Goedel pokazał na przykładzie abstrakcyjnych przekształceń na pozbawionych znaczenia symbolach, iż w ramach każdego systemu formalnego składającego się z aksjomatów i reguł wnioskowania istnieją prawdziwe zdania o tym systemie, których nie jesteśmy w stanie udowodnić przy pomocy środków tego systemu. Takim zdaniem jest np. „Tego stwierdzenia nie można udowodnić". Jaką wartość logiczną posiada to zdanie? Otóż gdyby było ono fałszywe, wówczas istniałby dowód tego stwierdzenia, a więc doszłoby do zaprzeczenia jego treści. Natomiast, gdyby nie istniał dowód tego stwierdzenia, to byłoby ono prawdziwe, gdyż to właśnie stwierdza. Mamy zatem prawdziwe stwierdzenie, którego nie można udowodnić. A to oznacza, że system jest niezupełny. Przedstawione zdanie nosi nazwę zdania Goedla. Dochodzimy zatem do wniosku, iż w każdym systemie formalnym dostatecznie silnym, by wyrazić wszystkie związki między liczbami naturalnymi, istnieją stwierdzenia nierozstrzygalne, których nie można udowodnić w ramach systemu, choć są to prawdziwe stwierdzenia o liczbach. Można się o tym przekonać wykraczając poza system. Goedel szybko skonstruował arytmetyczne stwierdzenie A, wyrażające matematycznie stwierdzenie: „arytmetyka jest niesprzeczna", po czym wykazał, że nie można tego stwierdzenia udowodnić, w związku z czym nie można udowodnić niesprzeczności arytmetyki, korzystając z dowolnego obejmującego arytmetykę systemu formalnego.

Znając idee najważniejszych pomysłów Goedla, spróbujmy prześledzić jego tok rozumowania:

1. opracowujemy system kodowania, który pozwala jednoznacznie przetłumaczyć dowolne wyrażenie logiczne i dowolny dowód z Principia Mathematica na jednoznacznie określone stwierdzenie dotyczące liczb naturalnych

2. zastępujemy pojęcie „prawdy" pojęciem „dowodliwości", przekształcamy paradoks Epimenidesa (paradoks kłamcy) w stwierdzenie: „Tego stwierdzenia nie da się udowodnić"

3. Wykazujemy, że w każdym systemie formalnym obejmującym arytmetykę, ma swój arytmetyczny odpowiednik — zdanie Godla G

4. Dowodzimy, że jeżeli system jest niesprzeczny, to zdanie Godla musi być prawdziwe. Stad wykazujemy niezupełność.

5. Wykazujemy, że nawet w wprowadzenie dodatkowych aksjomatów i stworzenie nowego systemu formalnego, w którym można udowodnić zdanie G, nie rozwiązuje problemu, gdyż w tym nowym systemie istnieje nowe zdanie Godla G, którego nie można udowodnić

6. Konstruujemy arytmetyczne stwierdzenie, które mówi, że „arytmetyka jest niesprzeczna". Dowodzimy, że tego arytmetycznego stwierdzenia nie można udowodnić, a zatem arytmetyka jako system formalny jest za słaba, by udowodnić własną niesprzeczność. ^{[ 6 ]}

Dla języka potocznego, twierdzi Tarski, również nie da się sformułować ścisłej, poprawnej definicji zdania prawdziwego. W języku tym najoczywistsza zdaje się być semantyczna definicja prawdy. Chodzi o definicję, która dałaby się po uproszczeniu zapisać: „zdanie prawdziwe jest to zdanie, które wyraża, że tak a tak rzeczy się mają, i rzeczy mają się tak właśnie". Ogólny schemat takiej definicji to: (*) "x jest zdaniem prawdziwym wtedy i tylko wtedy, gdy p", gdzie p oznacza jakiekolwiek zdanie, natomiast x nazwę jednostkową tego zdania. Tarski odwołuje się tu do definicji Arystotelesa: „Jest fałszem powiedzieć o tym, co nie jest, że jest, lub o tym, co jest, że nie jest; jest prawdą powiedzieć o tym, co jest, że jest lub o tym, co nie jest, że nie jest."

Tarski zastanawia się, jak należy zbudować nazwę zdania, aby w łatwy sposób można było podać zdanie, znając jego nazwę. Jako jedno z rozwiązań podaje nazwy cudzysłowowe. Nazwy cudzysłowowe składają się z cudzysłowów oraz wyrażenia pomiędzy cudzysłowami. Podstawiając do (*) nazwę cudzysłowową Tarski formułuje taki oto przykład: (**) „śnieg pada" jest zdaniem prawdziwym wtedy i tylko wtedy, gdy śnieg pada.

Drugim, wymienionym przez Tarskiego rodzajem nazw są nazwy strukturalnoopisowe, czyli nazwy opisujące, z jakich wyrazów składa się wyrażenie będące desygnatem nazwy, z jakich znaków składa się każdy poszczególny wyraz i w jakiej kolejności te znaki i wyrazy po sobie następują. Stąd wyprowadza definicję, znowu wstawiając do (*): wyrażenie, które składa się z dwóch wyrazów, z których pierwszy składa się z pięciu kolejnych liter: ś, n, i, e, g, zaś drugi z czterech kolejnych liter: p, a, d, a, jest zdaniem prawdziwym wtedy i tylko wtedy, gdy śnieg pada., a następnie uogólnia uogólnia (**) do następującej postaci: (***) dla dowolnego p — "p" jest zdaniem prawdziwym wtedy i tylko wtedy, gdy p oraz (****) dla dowolnego x — x jest zdaniem prawdziwym wtedy i tylko wtedy, gdy — dla pewnego p — x jest identyczne z "p" i przy tym p. Zauważa jednak, że nazwy cudzysłowowe można traktować jak pojedyncze wyrazy języka. W szczególności nazwa "p" jest niczym więcej niż tylko literą alfabetu. Chcąc uogólniać (**) nie otrzymamy (***) lub (****), a raczej zdanie: "p" jest zdaniem prawdziwym wtedy i tylko wtedy, gdy śnieg pada. Poza tym z (***) można wyprowadzić dwa sprzeczne wnioski: "p" jest zdaniem prawdziwym wtedy i tylko wtedy, gdy śnieg pada oraz "p" jest zdaniem prawdziwym wtedy i tylko wtedy, gdy śnieg nie pada. Podobnie tłumaczy, dlaczego nie można użyć nazwy strukturalnoopisowej dla sformułowania definicji zdania prawdziwego. W końcu Tarski formułuje dumny wniosek: próba zbudowania poprawnej definicji semantycznej wyrażenia „zdanie prawdziwe" dla języka potocznego napotyka bardzo istotne trudności. Widać, że nie znamy nawet ogólnej metody budowy takiej definicji. Po odrzuceniu definicji semantycznej pozostaje próba zbudowania definicji strukturalnej. Ogólny schemat takiej definicji to: zdanie prawdziwe to wyrażenie posiadające takie a takie własności strukturalne lub też dające się uzyskać z takich a takich strukturalnie opisanych wyrażeń przy pomocy takich a takich strukturalnych przekształceń. Zauważa, że nie potrafimy strukturalnie spośród wyrażeń języka wyróżnić tych, które są zdaniami, tym bardziej zaś nie umiemy wyodrębnić tych zdań, które są zdaniami prawdziwymi. To doprowadza go do wniosku, iż niemożliwe jest stworzenie strukturalnej definicji zdania prawdziwego dla języka potocznego. Sama możność konsekwentnego i przy tym zgodnego z zasadami logiki i duchem języka potocznego operowania wyrażeniem „zdanie prawdziwe" i, co za tym idzie, możność zbudowania jakiejkolwiek poprawnej definicji tego wyrażenia wydaje się mocno zakwestionowana. ^{[ 7 ]}

W książce Żegnaj, Kartezjuszu, znany amerykański matematyk, Keith Devlin, pisze, że jednym z najbardziej owocnych osiągnięć wczesnej fazy dwudziestowiecznej logiki matematycznej było znalezienie sposobu oddzielenia znaczenia od języka - sporządzenie ścisłego opisu semantyki formalnego języka matematycznego (znaczeń dobrze zbudowanych formuł tego języka) w odróżnieniu od jego składni (reguł gramatycznych tego języka). Logiczną teorię (matematycznego) znaczenia — klucz do oddzielenia znaczenia od języka zawdzięczamy właśnie Tarskiemu. Punktem wyjścia jego teorii jest bowiem proste, lecz bardzo istotne spostrzeżenie dotyczące każdego języka, formalnego lub naturalnego. Językowi samemu w sobie nie przysługują znaczenia. Znaczenie nie jest wewnętrzną własnością języka. Znaczenie słowa lub zdania zależy od tego, do czego to słowo lub zdanie się odnosi. Badania Tarskiego, z wyżej przedstawionych względów, dotyczyły tylko algebry czyli języka matematyki skończonego rzędu. W latach sześćdziesiątych próbowano przeprowadzić analogiczne analizy języków naturalnych, lecz sukcesy były ograniczone, gdyż teoria Tarskiego nie daje się automatycznie przenieść na ten teren. Można natomiast przenieść do badań nad językami naturalnymi ideę badań oddzielenia składni od semantyki. Praca Tarskiego stałą się w ten sposób inspiracją dla lingwistów, którzy w latach pięćdziesiątych w swoich badaniach nad językami naturalnymi oddzielili syntaktykę od semantyki. Umożliwiło to analizowanie i manipulowanie formułami symbolicznymi bez ograniczeń związanych z ich znaczeniem. Możemy zatem posługiwać się językiem w sytuacjach, gdy nie znamy znaczeń, a nawet gdy znaczeń tych nie ma.

Podczas zeszłego stulecia logicy wielokrotnie pokazali, że wiele można zyskać, nauczywszy się „pływać wśród symboli", tj. rozumować za pomocą manipulowania abstrakcyjnymi symbolami, uwolnionymi od znaczeń. W nowszych czasach techniki logiki abstrahujące od znaczenia umożliwiły nam programowanie komputerów — dla których nic nie posiada znaczenia — tak, by przeprowadzały one logiczne rozumowania. ^{[ 8 ]} Z komputerami potrafimy nawet wymieniać informacje i, jak się okazuje, nie zawsze potrafimy odróżnić, czy rozmawiamy z maszyną, czy z człowiekiem.  

*

Bibliografia:
Alfred Tarski, Pisma logiczno — filozoficzne, tom 1 — prawda, Warszawa 1995  
Keith Devlin, Żegnaj, Kartezjuszu, Warszawa 1999  
J. Casti, W. DePauli, Goedel, życie i logika, Warszawa 2003  
J. A. Stuchliński, Definicja zdania prawdziwego, Warszawa 2002.