|
Nauka » Matematyka i logika O prawdzie u Alfreda Tarskiego [1] Przypuśćmy,
że ktoś mówi: „Dziś w nocy widać milion gwiazd", a ktoś inny odpowiada: „To prawda"; wówczas — nic bardziej oczywistego — to, co powiedział pierwszy, jest prawdziwe wtedy i tylko wtedy, gdy prawdziwe jest to, co powiedział drugi. D. Davidson Prawda jak byt mieni się wielorako. W metafizyce mówi się o prawdzie ontycznej czyli „zgodności rzeczy z myślą" lub o prawdzie jako własności samego bytu. Teoria poznania odsyła do klasycznej definicji prawdy, zwanej Arystotelesowską, zgodnie z którą „prawdą jest powiedzieć o czymś, że jest, jeśli jest i że nie jest, jeśli nie jest" oraz definicji koherencyjnej i pragmatycznej. Za główne kryteria prawdy najczęściej przyjmuje się oczywistość, doświadczenie, praktykę lub poznawczą użyteczność. Wiek XX, to wiek, w którym głównym przedmiotem zainteresowania filozofów stał się język. Prawda zatem stała się zagadnieniem rozważanym przede wszystkim w obrębie semantyki. Do tego nurtu należą również poświęcone problemowi prawdy badania Tarskiego. Badania te, jak spróbuję krótko pokazać na końcu pracy, stały się inspiracją dla wielu współczesnych myślicieli. Tarski jest autorem dwóch teorii prawdy: syntaktycznej i semantycznej. Teoria syntaktyczna jest mniej znana i jej rozwój i praktyczne konsekwencje nie były przedmiotem zainteresowania wielu badaczy. Najlepsze jej rozwinięcie znajdujemy w systemach Leśniewskiego: prototetyce, ontologii i mereologii. Tworząc swoje systemy Leśniewski oparł się na definicji prawdy sformułowanej przez Tarskiego w jego pracy doktorskiej [ 1 ]: 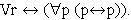
W powyższej syntaktycznej definicji, prawda jest równoważna elementarnej tautologii logicznego systemu. A ponieważ wszystkie systemy Leśniewskiego są zupełne i niesprzeczne, wobec tego każde zdanie prawdziwe można uzyskać jako tezę systemu. Oto definicja zdania prawdziwego w języku prototetyki (w pozostałych językach — ontologii i mereologii — definicja ta wygląda tak samo): 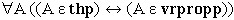
gdzie Semantyczna teoria prawdy Tarskiego często bywa opisywana jako wersja klasycznej definicji prawdy. Przedstawienie i badania związane z semantyczną teorią prawdy znajdują się wpracach Tarskiego, wydanych jako Pisma logiczno — filozoficzne, tom 1 — prawda. Główną tezą, którą uzasadnia i rozwija tam polski logik, jest stwierdzenie, że nie da się zbudować poprawnej definicji zdania prawdziwego dla języka potocznego oraz dla języków nieskończonego rzędu sformalizowanych nauk dedukcyjnych. Definicję taką można zbudować jedynie dla języka skończonego rzędu w systemie dedukcyjnym. [ 3 ] Tarski buduje definicję dla bardzo elementarnego systemu, stwierdzając, że można analogicznie zbudować podobną definicję w systemach bogatszych (ściślej: w takich, w których rząd zmiennej rozumiany w znaczeniu teorii typów nie przekracza pewnego z góry danego n będącego liczba naturalną). Zaczyna od rozróżnienia dwóch języków: języka, w którym mówimy, oraz języka, o którym mówimy. Zdanie, którego prawdziwość będziemy definiować, należy do języka, o którym mówimy. Sama definicja będzie jednak należeć do języka, w którym mówimy. Tarski tworzy zatem, bardzo prosty język, o którym mówimy. Zawiera on: trzy zmienne a, b, c, termin pierwotny „jest częścią", terminy logiczne: negację, alternatywę, kwantyfikator ogólny oraz nawiasy. Tarski nie podaje precyzyjnej aksjomatyki systemu, wyróżnia natomiast funkcje pierwszego rzędu (elementarne), czyli inkluzje (stwierdzenia „jest częścią"). Funkcje drugiego rzędu tworzymy łącząc funkcje pierwszego rzędu za pomocą jednego terminu logicznego. Analogicznie tworzy funkcje dowolnego rzędu naturalnego. Funkcje zdaniowe języka, o którym mówimy, nie posiadające zmiennych wolnych, noszą nazwę zdań. Język, w którym mówimy zawiera: wyrażenia równoznaczne z wyrażeniami języka, o którym mówimy (np. jest częścią, lub), wyrażenia z1, z2, z3 (które oznaczają kolejno zmienne a, b, c), funkcję nazwową I(x,y), której argumentami są z1, z2, z3, a wartościami odpowiednie inkluzje, wyrażenia: nieprawda, że x, suma logiczna x i y oraz generalizacja wyrażania y ze względu na x (np. (dla każdego x) y). In,p jest równoznaczne z I(zn,zp), gdzie n, p = 1, 2, 3. Chcąc skonstruować definicję zdania prawdziwego Tarski, posługuje się pojęciem spełniania funkcji zdaniowej przez ciąg przedmiotów. W sposób indukcyjny określamy, kiedy pewien ciąg przedmiotów spełnia funkcje zdaniową n - tego rzędu. W pierwszym kroku indukcyjnym stwierdzamy, że ciąg C spełnia inkluzję In,p wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) n, p = 1, 2, 3; (3) n — ty wyraz ciągu jest częścią p - tego wyrazu ciągu, czyli zachodzi inkluzja I(Cn,Cp). W drugim kroku Tarski stwierdza, że aby określić, kiedy ciąg C spełnia funkcje zdaniowe wyższego rzędu, należy jedynie określić, kiedy C spełnia negację, sumę i generalizację funkcji pewnego rzędu, jeśli wiadomo (z założenia indukcyjnego), że spełnia funkcje tego rzędu. C spełnia negację x wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) ciąg C nie spełnia x. C spełnia x + y wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) ciąg C spełnia x lub spełnia y. Ciąg C spełnia generalizację x ze względu na n-tą zmienna wtedy i tylko wtedy, gdy (1) C jest określony dla 1, 2, 3; (2) n, p = 1, 2, 3; (3) zarówno C, jak i każdy inny ciąg otrzymany z C przez zmianę tylko n — tego wyrazu, spełnia x. Zdania języka, o którym mówimy, są pewnymi funkcjami zdaniowymi, zatem możemy podać następującą definicję zdania prawdziwego: Zdanie z języka, o którym mówimy, jest prawdziwe wtedy i tylko wtedy, gdy każdy ciąg spełnia to zdanie. Definicja ta jest, zdaniem Tarskiego, dobra, ponieważ: (1) jest zgodna z intuicyjnym rozumieniem słowa prawdziwość; (2) jest przy niej spełniona zasada wyłączonego środka; (3) jest przy niej spełniona zasada sprzeczności; (4) pozwala udowodnić niesprzeczność rozważanego systemu. Jak zbudować definicję zdania prawdziwego w pewnych systemach dedukcyjnych skończonego rzędu Tarski pokazuje na przykładzie języka algebry klas. Ważnym elementem tej definicji jest umowa P, która powiada: poprawną formalnie definicję symbolu „Vr" (klasa wszystkich zdań prawdziwych), sformułowaną w terminach metajęzyka, nazywać będziemy trafną definicję prawdy, o ile pociąga ona za sobą następujące konsekwencje: (a) wszystkie zdania dające się uzyskać z wyrażenia „x należy do Vr wtedy i tylko wtedy, gdy p" przez zastąpienie symbolu „x" nazwą strukturalnoopisową dowolnego zdania rozważanego języka, zaś symbolu "p" — wyrażeniem, stanowiącym przekład tego zdania na metajęzyk; (b) zdanie "dla dowolnego x — jeśli x należy do Vr, to x należy do S" lub innymi słowy, "Vr należy do S". [ 4 ] Aby uzasadnić, że nie da się skonstruować definicji prawdy dla wszystkich języków nieskończonego rzędu, Tarski powołuje się na logika austriackiego, Kurta Goedla. Wykazał on, że w jednym z takich języków — arytmetyce, nie da się skonstruować ścisłej definicji prawdy. Twierdzenie Goedla w wersji formalnej brzmi: w każdym niesprzecznym systemie formalnym obejmującym arytmetykę istnieją arytmetyczne prawdy, których nie można udowodnić w ramach tego systemu. Twierdzenie to ma dwie wersje: pierwszą mówiącą o niezupełności systemów dedukcyjnych zawierających arytmetykę liczb naturalnych oraz drugą stwierdzającą niemożliwość przeprowadzenia dowodu niesprzeczności (spójności) systemów zawierających arytmetykę liczb naturalnych przy pomocy środków samych tych systemów. Dowód twierdzenia Goedla jest bardzo skomplikowany, dlatego spróbuję tylko przybliżyć jego ideę. Goedel zwrócił uwagę, iż każdy system formalny dowolnej dziedziny matematyki sam też jest obiektem matematycznym. Można zatem arytmetycznie przedstawić dowolny system formalny, który ma obejmować arytmetykę. Mówiąc inaczej, znalazł sposób przedstawienia wszystkich stwierdzeń o liczbach i związkach między liczbami za pomocą liczb. [ 5 ]. Goedel wprowadził taki wariant numerowania, by zakodować wszystkie możliwe stwierdzenia arytmetyczne w języku samej arytmetyki. Punktem wyjścia były dla niego „Principia Mathematica" B. Russella i Alfreda Northa Whiteheada, które były próbą zapisu matematyki jako zaksjomatyzowanego systemu formalnego. Goedel określił sposób arytmetycznego kodowania wszystkich symboli i stwierdzeń języka Russella — Whiteheada. Założył, że istnieje 10 znaków logicznych, którym odpowiadają pewne numery (nazwane później numerami Goedla) — liczby całkowite od 1 do 10:
Oprócz tych elementarnych zmiennych język „Principia Mathematica" zawierał zmienne logiczne łączone za pomocą znaków. Zmienne te można podzielić na trzy rodzaje:
Przypisy: [ 1 ] Józef Andrzej Stuchliński, Definicja
zdania prawdziwego, Warszawa 2002, s.220 — 222. [ 2 ] Ibidem, s.218. [ 3 ] Alfred
Tarski, Pisma logiczno -
filozoficzne, Warszawa 1995, s.9 — 11. [ 4 ] Ibidem, s.60 — 61. [ 5 ] Ten sposób myślenia nie
jest nowy — np. o języku polskim mówimy po polsku. « Matematyka i logika (Publikacja: 24-08-2004 )
str. 3573 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [ Regulamin publikacji ] [ Bannery ] [ Mapa portalu ] [ Reklama ] [ Sklep ] [ Zarejestruj się ] [ Kontakt ] Racjonalista © Copyright 2000-2018 (e-mail: redakcja | administrator) | ||



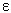 oznacza „jest", thp
oznacza „teza prototetyki", vrpropp
oznacza „zdanie prawdziwe". Słownie: dla każdego A, A jest tezą
prototetyki wtedy i tylko wtedy, gdy A jest zdaniem prawdziwym.
oznacza „jest", thp
oznacza „teza prototetyki", vrpropp
oznacza „zdanie prawdziwe". Słownie: dla każdego A, A jest tezą
prototetyki wtedy i tylko wtedy, gdy A jest zdaniem prawdziwym.